Hvad er binær? [Teknologi forklaret]

Reklame

I betragtning af at binær er så absolut grundlæggende for eksistensen af ​​computere, forekommer det underligt, at vi aldrig har taklet det emne før - så i dag troede jeg, at jeg ville give et kort overblik over, hvad binært faktisk betyder, og hvordan det bruges i computere. Hvis du altid har spekuleret på, hvad der er forskellen mellem 8-bit, 32-bit, og 64-bit det er virkelig, og hvorfor det betyder noget - så læs videre!

Hvad er binært? Forskellen mellem Base 10 og Base 2

De fleste af os er vokset op i en base 10-verden af ​​numre, som jeg mener, at vi har 10 ’Base’ tal (0-9) hvorfra vi stammer alle andre tal. Når vi er opbrugt, flytter vi et enhedsniveau op - 10'erne, 100'erne, 1000'erne - denne form for tælling hamres i vores hjerner fra fødslen. Faktisk var det først fra den romerske periode, at vi begyndte at tælle i base 10. Før det var base 12 den nemmeste, og folk brugte deres knoker til at tælle.

Når vi lærer base 10 i folkeskolen, skriver vi ofte enhederne sådan:

Så antallet

1990 består faktisk af 1 x 1000, 9 x 100, 9 x 10, og 0 x 1. Jeg er sikker på, at jeg ikke behøver at forklare base 10 længere end det.

Men hvad nu, i stedet for at have et komplet udvalg af 0,1,2,3,4,5,6,7,8,9 at arbejde med som basisnumre - hvad hvis vi kun havde det 0, og 1. Dette kaldes base 2; og det kaldes også ofte binær. I en binær verden kan du kun tælle 0,1 - så skal du gå til næste enhedsniveau.

Tæller i binær

Det hjælper enormt, hvis vi skriver enhederne ud, når vi lærer binært. I dette tilfælde multipliceres den i stedet for at hver ekstra enhed ganges med 10, hvilket giver os 1,2,4,8,16,32,64... Så for at hjælpe med at beregne, kan vi skrive dem sådan ud:

Med andre ord repræsenterer den højeste værdi i et binært tal hvor mange 1'er. Det næste ciffer til venstre for det repræsenterer hvor mange 2'er. Det næste repræsenterer hvor mange 4'er... og så.

Med denne viden kan vi udskrive en tabel med tælling i binær med den ækvivalente base 10-værdi angivet til venstre.

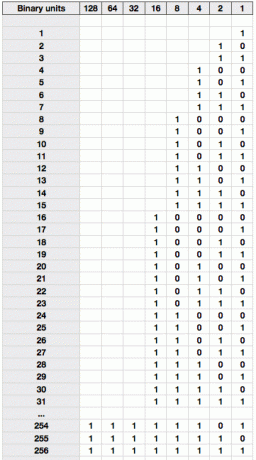
Brug et øjeblik på at gå over det, indtil du kan se nøjagtigt, hvorfor 25 er skrevet som 11001. Du skal være i stand til at nedbryde det som værende 16 + 8 + 1 = 25.

Arbejde bagud - base 10 til binær

Du skal nu være i stand til at finde ud af, hvilken værdi et binært tal har ved at tegne en lignende tabel og multiplicere hver enhed. At skifte et almindeligt base 10-nummer til binært kræver lidt mere indsats. Det første trin er at finde den største binære enhed, der "passer ind" i antallet. Så hvis vi for eksempel gjorde 35, så er det største antal fra den tabel, der passer til 35, 32, så vi ville have en 1 der i den kolonne. Vi har derefter en rest på 3 - som ville have brug for en 2, og derefter til sidst en 1. Så vi får 100011.

8-bit, Bytes og Octets

Tabellen, jeg har vist ovenfor, er 8-bit, fordi vi maksimalt har 8 nuller og en til at bruge til vores binære nummer. Således er det maksimale antal, vi muligvis kan repræsentere 11111111, eller 255. Dette er grunden til at repræsentere et hvilket som helst tal fra 0-255, vi har brug for mindst 8-bit. Octet og Byte er simpelthen en anden måde at sige 8-bit på. Derfor 1 byte = 8 bit.

32 vs 64-bit computing

I dag hører du ofte betingelserne 32-bit og 64-bit versioner af Windows, og du ved måske, at 32-bit Windows kun kan understøtte op til 4 gigabyte RAM. Hvorfor er det dog?

Det hele kommer ned på hukommelsesadressering. Hver hukommelsesbit har brug for en unik adresse for at få adgang til den. Hvis vi havde en 8-bit hukommelsesadresseringssystem, ville vi kun have et maksimum på 256 byte hukommelse. Med en 32-bit hukommelsesadresseringssystem (forestil dig at udvide tabellen ovenfor til at have 32 binære enhedssøjler), kan vi gå hvor som helst op til 4,294,967,296? 4 milliarder byteseller med andre ord - 4 GIGAbyte.64-bit computing fjerner i det væsentlige denne grænse ved at give os op til 18 kvintillioner forskellige adresser - et antal, som de fleste af os simpelthen ikke kan forstå.

IPv4-adressering

Den seneste bekymring i computerverdenen er alt om IP-adresser IPv6 & The Coming ARPAgeddon [Technology Explained] Læs mere , i særdeleshed IPv4 adresser som disse:

• 192.168.0.1
• 200.187.54.22

De består faktisk af 4 numre, der hver repræsenterer en værdi op til 255. Kan du gætte hvorfor? Jej, hele adressen er repræsenteret af 4 oktetter (32 bit i alt). Dette virkede som en frygtelig masse mulige adresser (faktisk omkring 4 milliarder) på det tidspunkt, hvor internettet først blev opfundet, men vi er hurtigt ved at løbe ud nu, hvor alt i vores liv skal tilsluttes. For at løse dette bruger den nye IPv6 128 bit i alt, hvilket giver os ca. 340 undecillion (sæt 38 nuller i slutningen) adresser at lege med.

Jeg vil lade det være der i dag, så jeg kan vende tilbage til mit oprindelige mål, som var at skrive den næste Arduino-tutorial - hvor vi udnytter meget af et bitskiftregister. Jeg håber i dag har givet dig en grundlæggende forståelse af, hvordan binære er så betydningsfulde for computere, hvorfor de samme numre fortsat vises, og hvorfor antallet af bit, vi er nødt til at repræsentere noget, sætter en begrænset grænse for mængden af ​​hukommelse, skærmstørrelse, mulige farveværdier eller unikke IP-adresser, der er tilgængelige for os. Næste gang skal vi se på binære logikberegninger, hvilket er stort set alt, hvad en computerprocessor gør, samt hvordan computere kan repræsentere negative tal.

Kommentarer? Forvirring? Fandt du, at min forklaring var let at forstå? Uanset hvad, så kontakt venligst kommentarerne. Jeg forlader dig med en binær vittighed!

Der er kun 10 typer mennesker i verden: dem, der forstår binær, og dem, der ikke gør det.

Billedkredit: Shutterstock