7 algoritmer enhver programmerer bør vide

Som studerende i programmering har du sandsynligvis lært masser af forskellige algoritmer i løbet af din karriere. At blive dygtig til forskellige algoritmer er helt afgørende for enhver programmør.

Med så mange algoritmer kan det være udfordrende at holde styr på, hvad der er vigtigt. Hvis du forbereder dig til et interview eller bare pudser dine færdigheder, vil denne liste gøre det relativt let. Læs videre, da vi viser de mest vigtige algoritmer til programmører.

1. Dijkstra's algoritme

Edsger Dijkstra var en af ​​hans tids mest indflydelsesrige dataloger, og han bidrog til mange forskellige områder inden for computervidenskab, herunder operativsystemer, kompileringskonstruktion og meget mere. Et af Dijkstras mest bemærkelsesværdige bidrag er opfindsomheden i hans korteste sti -algoritme til grafer, også kendt som Dijkstras korteste sti -algoritme.

Dijkstras algoritme finder den enkelt korteste sti i en graf fra en kilde til alle grafhjørner. Ved hver iteration af algoritmen tilføjes et toppunkt med minimumsafstanden fra kilden og en, der ikke findes på den nuværende korteste vej. Dette er den grådige ejendom, der bruges af Djikstras algoritme.

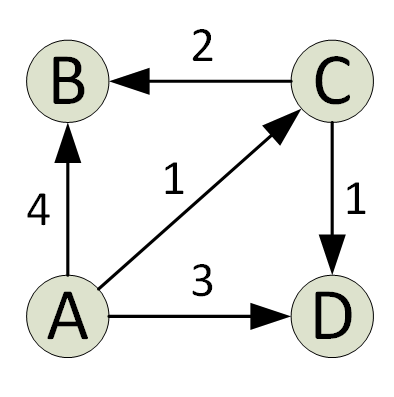
Algoritmen implementeres typisk ved hjælp af et sæt. Dijkstras algoritme er meget effektiv, når den implementeres med en Min Heap; du kan finde den korteste sti på bare O (V+ElogV) tid (V er antallet af hjørner og E er antallet af kanter i en given graf).

Dijkstra's algoritme har sine begrænsninger; det fungerer kun på rettede og uorienterede grafer med kanter med positiv vægt. For negative vægte er Bellman-Ford-algoritmen typisk at foretrække.

Interviewspørgsmål inkluderer normalt Djikstras algoritme, så vi anbefaler stærkt at forstå dens indviklede detaljer og applikationer.

2. Flet sorter

Vi har et par sorteringsalgoritmer på denne liste, og fletningssortering er en af ​​de vigtigste algoritmer. Det er en effektiv sorteringsalgoritme baseret på programmeringsteknikken Divide and Conquer. I værste fald kan fletningssortere sortere “n” tal på bare O (nlogn) tid. Sammenlignet med primitive sorteringsteknikker som f.eks Boblesortering (det tager O (n^2) tid), fletningssort er fremragende effektiv.

Relaterede: Introduktion til flette sorteringsalgoritme

I fletningssortering opdeles matrixen, der skal sorteres, gentagne gange i underarrays, indtil hvert delarray består af et enkelt tal. Den rekursive algoritme fletter derefter gentagne gange delarrayene og sorterer arrayet.

3. Quicksort

Quicksort er en anden sorteringsalgoritme baseret på programmeringsteknikken Divide and Conquer. I denne algoritme vælges først et element som pivot, og hele arrayet opdeles derefter omkring denne pivot.

Som du sikkert har gættet, er en god omdrejningspunkt afgørende for en effektiv sortering. Pivoten kan enten være et tilfældigt element, medieelementet, det første element eller endda det sidste element.

Implementeringer af quicksort er ofte forskellige i den måde, de vælger en pivot. I det gennemsnitlige tilfælde sorterer quicksort et stort array med en god pivot på bare O (nlogn) tid.

Den generelle pseudokode for quicksort opdeler gentagne gange arrayet på pivoten og placerer det i den korrekte position for delarrayet. Det placerer også elementerne mindre end pivoten til venstre og elementerne større end pivoten til højre.

4. Dybde Første søgning

Depth First Search (DFS) er en af ​​de første grafalgoritmer, som eleverne underviser i. DFS er en effektiv algoritme, der bruges til at krydse eller søge i en graf. Det kan også ændres til at blive brugt i trætraversal.

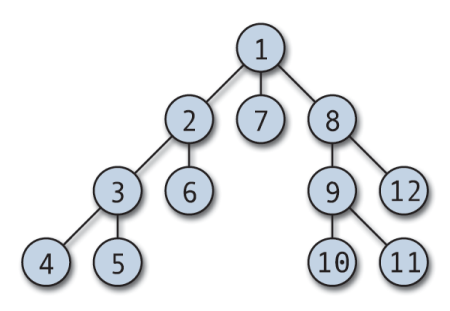
DFS -traversal kan starte fra enhver vilkårlig node, og den dykker ned i hvert tilstødende toppunkt. Algoritmen går tilbage, når der ikke er noget ubesøgt toppunkt, eller hvis der er en blindgyde. DFS implementeres typisk med en stak og et boolsk array for at holde styr på de besøgte noder. DFS er enkel at implementere og usædvanligt effektiv; det virker (V+E), hvor V er antallet af hjørner og E er antallet af kanter.

Typiske anvendelser af DFS -traversal omfatter topologisk sortering, detektering af cyklusser i en graf, stifinding og finde stærkt forbundne komponenter.

5. Bredde-første søgning

Breadth-First Search (BFS) er også kendt som en niveauordre-traversal for træer. BFS fungerer i O (V+E) svarende til en DFS -algoritme. BFS bruger imidlertid en kø i stedet for stakken. DFS dykker ned i grafen, mens BFS krydser grafen i bredden.

BFS -algoritmen anvender en kø for at holde styr på hjørnerne. Ubesøgte tilstødende hjørner besøges, markeres og står i kø. Hvis toppunktet ikke har nogen tilstødende hjørne, fjernes et hjørne fra køen og undersøges.

BFS bruges almindeligvis i peer-to-peer-netværk, den korteste vej for en uvægtet graf og til at finde det mindste spændende træ.

6. Binær søgning

Binær søgning er en simpel algoritme til at finde det nødvendige element i et sorteret array. Det fungerer ved gentagne gange at dele matrixen i to. Hvis det krævede element er mindre end det midterste element, behandles venstre side af det midterste element yderligere; ellers halveres højre side og søges igen. Processen gentages, indtil det nødvendige element er fundet.

Tidskompleksiteten i værste tilfælde af binær søgning er O (logn), hvilket gør den meget effektiv til at søge lineære arrays.

7. Mindste spændvidde -algoritmer

Et minimumspændingstræ (MST) i en graf har minimumsomkostningerne blandt alle mulige spantræer. Prisen på et spændende træ afhænger af vægten af ​​dets kanter. Det er vigtigt at bemærke, at der kan være mere end et minimumstrækningstræ. Der er to hoved -MST -algoritmer, nemlig Kruskal's og Prim's.

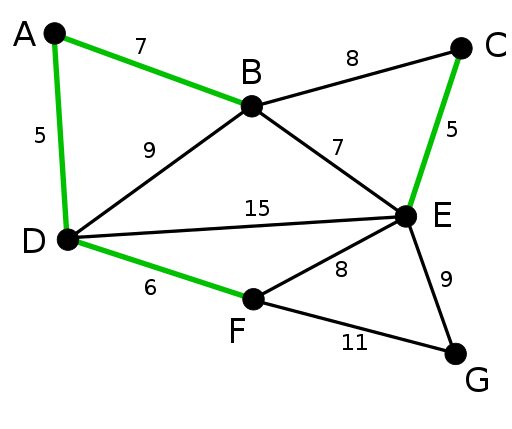
Kruskals algoritme skaber MST ved at tilføje kanten med minimale omkostninger til et voksende sæt. Algoritmen sorterer først kanter efter deres vægt og tilføjer derefter kanter til MST startende fra minimum.

Det er vigtigt at bemærke, at algoritmen ikke tilføjer kanter, der danner en cyklus. Kruskals algoritme foretrækkes til sparsomme grafer.

Prim's algoritme bruger også en grådig egenskab og er ideel til tætte grafer. Den centrale idé i Prims MST er at have to forskellige sæt hjørner; et sæt indeholder den voksende MST, mens det andet indeholder ubrugte hjørner. På hver iteration vælges den mindste vægtkant, der forbinder de to sæt.

Minimumspændende træalgoritmer er afgørende for klyngeanalyse, taksonomi og broadcast -netværk.

En effektiv programmerer er god til algoritmer

Programmører lærer og udvikler konstant deres færdigheder, og der er nogle grundlæggende væsentlige ting, som alle skal være dygtige til. En dygtig programmør kender de forskellige algoritmer, fordele og ulemper ved hver enkelt, og hvilken algoritme der er mest passende til et givet scenario.

En introduktion til shell -sorteringsalgoritmen

Selvom skalsortering ikke er den mest effektive metode, har begyndere meget at vinde på at øve den.

Læs Næste

Om forfatteren